Sunday, June 19, 2011

Up Close And Out Of Focus (mostly)

So, why is it that there is so little depth of field when photographing portraits when photographing mountains and nearby fences is relatively easier?

The formula for Depth of field (at least one of them anyway) is:
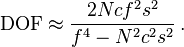
\mathrm {DOF} \approx \frac {2 N c f^2 s^2} {f^4 - N^2 c^2 s^2} \,.
where N if the f number, f is the focal length, c is the circle of confusion and s is the distance the camera is focused. Note that in the formula, depth of field varies as the square of the subject distance. That means that if we have 2 feet in front of the subject distance of 10 feet, we'd not have one foot if we were shooting at five feet, we'd have six inches, one quarter - so moving in close hugely affects depth of field. Changing focal length of lenses complicates things, but this explains the typical depth of field scale on an old fashioned prime lens - with almost no useable depth at near focus, and fairly decent depth at the longer distances.

The formula came from Wikipedia
Posted by at

7 comments:

TJ said...

Oh man... Physics and formulas again.
I was trying for ages to memorize the hyperfocal distance formula, and guess what; a fail. I still can't remember a character.
The irony is, I'm a physics graduate!

10:06 pm
Tim said...

You've reminded me of an utterance by a photo-club judge: "If you'd focussed a third of the way in, that would be hyperfocussing and everything would be sharp". The subject-matter: a table-top flower still-life about 10-30cm away where hyperfocussing would require f/1024 or narrower, guaranteeing *nothing* sharp.

Thanks for throwing that idiocy into sharper relief. I know who I'd rather believe ;)

3:23 am
Tien Frogget said...

Haha, this is total greek to me. We as photographers are so spoiled nowadays with our fancy digital cameras... it's so much easier now than it used to be to take great photos without having to know all the physics and formulas.

12:48 pm
Chuck Kimmerle said...

it's so much easier now than it used to be to take great photos without having to know all the physics and formulas

I never knew a single photographer who knew this formula by heart. It's great for understanding why DOF works the way it does, but it little or no practical application for those of us who jockey a camera. Now, if George can find the formula for good images, I'll try and remember that one.

10:43 am
Anonymous said...

I am not interested in the hairs on your warts; I want to see into your eyes. Need but a little DOF for that (even though I do like to see where the nose ends...).

Enter the formula into Excel, make some plots and carry them laminated with you. However, you'll find that the "constant" of the formula is kind of arbitrary. Anyway, there's also an A_dep setting on your camera...

3:41 am
Anonymous said...

We as photographers are so spoiled nowadays with our fancy digital cameras... it's so much easier now than it used to be to take great photos without having to know all the physics and formulas.
Sorry, mate. The laws of physics apply to digital cameras as well as they did to the "old" analog ones. You don't have a digital lens, it's still glass, it's still refraction, focal length, aperture and eventually diffraction, too. Nobody needs to keep that formula in mind, but knowing the fod is proportional to one over square of focal lenght helps understanding. As well as getting to know your lenses does.

Cheers
Henkki

10:24 am
Anonymous said...

For the fun of it: As long as your object is significantly closer than the hyperfocal distance, the term f^4 is much bigger than N^2c^2s^2. Hence you can in ignore the latter in this cases. Then the formula gets reduced to:

2Ncs^2/f^2

Not exact any longer, but a pretty good approximation.

What does this tell us? Well, the DOF increases with the square of the distance. And it increases when we close the aperture.

Let us compare the approximated value and the correct value assuming c equals 0.03 mm. If I used my 85 mm f/1.8 fully open to shoot a portrait from a distance of 1.5 m, the correct value would be a DOF of 33.64 mm, the approximated value one of 33.63. Not much difference and explains why in this case the tip of the nose looks blurred already when I get the focus spot-on the eyes. If I want the nose sharp, I'll have to stop down to 5.6, giving me a DOF of 104.76 mm (approx. 104.64). That is good to know (and matches with my experience).

Different example: I want to take a shot of a belltower from a distance of 50 m with f set to 24 mm. Can I use the approximation? Definitely not, as the hyperfocal distance is that short for all f-numbers I can set, the 50 m will be more.

Completely different again when using telephoto lenses. Say I have a 500 mm I want to use at f/8. What is the hyperfocal distance now? Believe it or not, over a kilometre. So the approximation will be good for anything much closer than that, say 100 m.

Boring? Maybe, not for me, pretty useful I think.

12:17 pm

Post a Comment

Subscribe to: Post Comments (Atom)